A brief discussion of the Practical Byzantine Fault Tolerance (PBFT) algorithm

Marton Trencseni - Sat 06 September 2025 - Distributed

Introduction

In my previous articles I explored Lamport’s famous Byzantine Generals problem and the algorithms he proposed for solving it. We looked first at the “oral-messages” version, where generals pass claims about what others said, and then at the signed-messages version, where cryptographic signatures simplify the problem. These algorithms are mathematically elegant, but they were not designed with real distributed systems in mind. They serve more as proofs of possibility than blueprints for implementation.

By the late 1990s, however, researchers were asking a practical question: could Byzantine fault tolerance actually be made efficient enough to run a real service? At OSDI ’99, Miguel Castro and Barbara Liskov answered “yes” in their paper Practical Byzantine Fault Tolerance. This was a turning point — PBFT was the first system to demonstrate that Byzantine consensus could run with near-production performance.

This post positions PBFT relative to Lamport’s original algorithms. We’ll see how it improves on the signed-messages approach, how the protocol works in practice, what problems it does and doesn’t solve, how it compares to Paxos and crash-fault tolerant systems, and finally why PBFT and its descendants are so relevant in the blockchain era.

Previous articles on Bytepawn on Byzantine Fault Tolerance:

Research literature:

Paxos-related papers:

PBFT vs. Lamport’s algorithm

Lamport’s oral-messages algorithm was groundbreaking but expensive. To tolerate $M$ faulty nodes, it required $N \geq 3M+1$ total nodes, and communication happened through an exponential cascade of messages. Signed messages improved things: because signatures prevent equivocation, the requirement drops to $N \geq M+2$. The algorithm also becomes easier to reason about, since forwarding signed messages avoids much of the recursive claim-checking.

But neither of Lamport’s solutions is “practical.” They assume a model of generals shouting across the battlefield, rather than servers on a network running a replicated service. Message cascades are conceptually elegant, but in practice they are wasteful and hard to implement efficiently. What was missing was a way to collapse the cascade into a smaller, structured set of messages while preserving Byzantine safety.

PBFT achieves exactly this. It introduces the concept of a primary (leader), responsible for ordering client requests, while backups confirm and cross-check. Instead of flooding the system with cascades, PBFT uses quorum-based phases — pre-prepare, prepare, and commit — to reach agreement. It also optimizes cryptography: instead of signatures on every message, it uses lightweight message authentication codes (MACs) in normal operation, with signatures only in rare view-change events. The result is $O(n^2)$ message complexity instead of exponential, and performance close to unreplicated systems.

MACs are a kind of cryptographic checksum computed with a shared secret key between two replicas. They are significantly faster to generate and verify than digital signatures, and they keep message sizes small. The trade-off is that they don’t provide non-repudiation — since both parties know the secret, either could have produced the MAC. But in PBFT’s setting, that’s acceptable: replicas only need to authenticate messages between themselves, not prove their origin to outside parties. By relying on MACs for the common case and reserving expensive signatures for rare events like view-changes, PBFT achieves the efficiency needed for practical deployment.

How PBFT works

At the heart of PBFT is a three-phase protocol. When a client submits a request, the current primary assigns it a sequence number and broadcasts a pre-prepare message with that proposal. Each backup verifies the proposal and then issues a prepare message to all others. Once a replica sees enough matching prepare messages, it knows the group is converging and sends a commit message. Finally, once a replica sees enough commits, it executes the request and replies to the client.

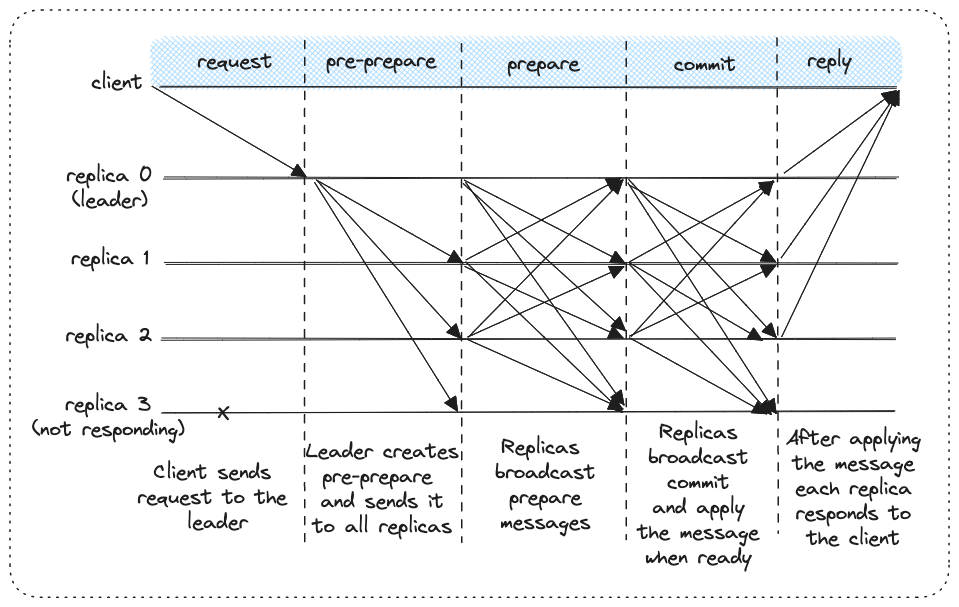
The message count in PBFT scales as $O(n^2)$ because every phase of the protocol requires replicas to broadcast to all other replicas. In the prepare phase, for example, each of the $n-1$ backups sends a prepare message to every other replica, resulting in roughly $(n-1)^2$ transmissions. The commit phase has the same pattern: once a replica is prepared, it multicasts a commit to all $n$ nodes, and again everyone must collect $2f+1$ matching commits. With both prepare and commit involving all-to-all communication, the overall number of messages per request grows proportionally to $n^2$. This quadratic scaling is manageable for small groups (e.g., a consortium of 4–20 replicas), but it becomes a bottleneck at hundreds or thousands of participants, which is why large-scale blockchain protocols adapt PBFT with committee sampling or other techniques.

This pipeline of pre-prepare → prepare → commit ensures safety: even if the primary is malicious and tries to equivocate, the honest replicas only move forward when they see enough agreement across the group. The quorum thresholds are chosen so that no two conflicting proposals can both be accepted — any two quorums overlap in at least one honest node.

PBFT also includes mechanisms to handle a faulty or slow leader. If replicas notice a lack of progress, they initiate a view-change: the system increments the view number and selects a new primary in round-robin fashion. To prevent unbounded growth of logs, PBFT adds checkpoints, where replicas agree on a hash of the current state at regular intervals and discard old protocol messages. These optimizations ensure the system can run indefinitely without exhausting memory or storage.

What PBFT solves and what it doesn’t

PBFT’s core achievement is to make Byzantine consensus practical. It ensures that all honest replicas agree on the same sequence of requests, even if some replicas are actively malicious. It prevents equivocation and double execution, and it maintains liveness: clients eventually get responses as long as fewer than a third of replicas are faulty. For distributed services that must survive arbitrary node failures, this was a breakthrough.

However, PBFT does not solve every problem. Importantly, it does not filter the content of client requests. If an authorized client issues a harmful request — DROP database or Transfer $1M to the hacker's account — PBFT will faithfully replicate it across all nodes. The protection is at the level of consistency, not application semantics. Application-level security (authentication, authorization, business logic) is still required.

PBFT also assumes a fixed, known set of replicas. It does not prevent Sybil attacks, where one adversary pretends to be many nodes. It requires $3f+1$ replicas to tolerate $f$ faults, which is expensive compared to Paxos’s $2f+1$. And like any system, if all replicas run the same buggy software, no consensus protocol can save you — they will all fail in the same way. PBFT narrows the attack surface but does not eliminate it.

Paxos vs. PBFT: Crash vs. Byzantine Fault Tolerance

A natural question is: why not just use Paxos or Raft? These crash-fault tolerant (CFT) protocols already power Google Spanner, Zookeeper, Etcd, and countless production systems. They assume nodes may crash or be partitioned, but not lie. They require only $2f+1$ replicas to tolerate $f$ failures, and their protocols are simpler. For most single-organization deployments, CFT is “good enough.”

Note: Paxos will later be covered in this series on distributed algorithms.

PBFT is heavier: it needs $3f+1$ replicas, more message exchanges, and more cryptographic checks. But it tolerates a stronger adversary model: replicas that equivocate, collude, or act maliciously. This matters in environments where not all nodes are under one administrator’s control, or where insider compromise is a real threat.

This tension has shaped the debate for 25 years. In trusted, enterprise settings, Paxos and Raft dominate because they are efficient and sufficient. In adversarial or federated settings, BFT protocols are necessary despite the cost. The question is always: what is your threat model? Do you worry only about crashes, or also about active lies?

A useful way to see how these approaches relate is side by side:

Algorithm Fault Model Node Requirement Message Pattern Cryptography Used Finality Practical Use
Lamport Oral-Messages Byzantine $N \geq 3M+1$ Exponential cascade None Deterministic Theory only
Lamport Signed-Messages Byzantine $N \geq M+2$ Cascade (but deduplicates) Digital Signatures Deterministic Theory / teaching
PBFT Byzantine $N \geq 3f+1$ Three-phase, $O(n^2)$ MACs + Signatures (rare) Deterministic Practical systems, blockchains
Paxos Crash-only (not Byzantine) $N \geq 2f+1$ Two-phase, $O(n)$ None (auth assumed) Deterministic Production systems (Spanner, etc.)

This makes clear how Lamport’s original algorithms provided proofs of possibility, PBFT compressed those ideas into a practical protocol with quadratic communication, and Paxos dominate when only crash faults are in scope.

PBFT in Blockchains

Blockchains brought BFT back into the spotlight. In Bitcoin and Ethereum, consensus is probabilistic, driven by Proof-of-Work. Blocks may fork, and “finality” is only statistical — the deeper a block is buried, the safer it is. This is fine for open, permissionless systems, but it is inefficient and slow. Permissioned blockchains, where validators are known entities (e.g., banks, companies), don’t need mining. Instead, they can use PBFT-style consensus for deterministic finality.

A key difference is finality. In PBFT, once a quorum commits a block, it is final immediately — no alternative history can ever be accepted. In Bitcoin or Ethereum’s Proof-of-Work model, finality is probabilistic: even after six confirmations, there remains a tiny chance of reorganization if a longer chain appears. This distinction is crucial in financial or enterprise contexts, where immediate, irreversible confirmation is often required.

PBFT ensures that once a block is committed, it cannot be reversed, and that all honest validators have the same chain. This strong finality is attractive for financial and enterprise use cases, where forks are unacceptable. Systems like Hyperledger Fabric initially relied on PBFT for ordering, and protocols like Tendermint directly adapt PBFT’s pre-prepare/prepare/commit into the blockchain setting. Tendermint adds rounds and timeouts, but the core idea is pure PBFT: a leader proposes, validators vote twice, and the block is finalized.

One important difference is that public blockchains like Bitcoin and Ethereum have no permanent leaders. Instead, leader election is randomized by mining puzzles (Proof-of-Work) or stake-weighted lotteries (Proof-of-Stake). This avoids reliance on a single replica to drive progress, at the cost of probabilistic rather than deterministic guarantees. In PBFT, the primary role is explicit and rotates deterministically on view-change; in blockchains, leadership is temporary and emerges stochastically from economic resources.

Another difference is how “malicious values” are handled. In PBFT, replicas do not inspect the semantics of client requests — a harmful but valid command will be executed consistently. In blockchains, every full node independently validates all transactions before accepting a block. Invalid transactions (e.g., double-spends, or spending without a signature) are rejected, regardless of what miners or validators propose. This split between consensus (ordering) and validation (correctness) ensures that “transfer all BTC to me” can never enter the chain unless it passes the same rules every node enforces.

The limitation remains scalability. PBFT requires $O(n^2)$ message exchanges among validators. This is fine for a consortium of 10 banks, but problematic for 10,000 public validators. That is why blockchains pair PBFT-style finality with mechanisms like proof-of-stake or committee sampling, which limit the number of participants in each round. Sybil resistance is also essential: unlike PBFT’s fixed replica set, open blockchains must ensure identities can’t be faked cheaply, hence proof-of-work and proof-of-stake.

In short, PBFT is the intellectual ancestor of modern blockchain consensus: it showed that Byzantine agreement could be practical. Even if we don’t deploy PBFT “as is,” its principles — signatures, quorums, view-changes — are woven into the DNA of blockchain consensus protocols today.

Conclusion

Lamport gave us the theoretical foundation: oral-messages for possibility, signed-messages for simplicity. Castro and Liskov gave us PBFT, a protocol that made Byzantine consensus practical for the first time. It compresses the message cascade into three structured phases, optimizes cryptography, and demonstrated near-production performance.

PBFT is not a silver bullet. It doesn’t prevent bad application-level requests, it assumes a fixed replica set, and it is more costly than Paxos. But in environments where malicious behavior is a concern — federated systems, financial ledgers, blockchains — it provides guarantees that CFT cannot.

Twenty-five years on, the tension between CFT simplicity and BFT robustness still defines consensus design. PBFT stands as the bridge between Lamport’s theory and today’s blockchain protocols: a proof that Byzantine consensus is not just possible, but practical.

lamport byzantine generals distributed signed signature pbft blockchain paxos raft