Random numbers, the natural logarithm and higher dimensional simplexes

Introduction

This is a fun post to exercise our brain and practice college math.

Let's play a game: draw a uniform random number between 0 and 1. What is the expected value?

from random import random

def once(n=1000*1000):
    sum = 0.0
    for _ in range(n):
        sum += random()
    return sum/n
print(once())

> 0.50023

As expected, it's 0.5.

Okay, what about if we draw two numbers?

def twice(n=1000*1000):
    sum = 0.0
    for _ in range(n):
        sum += random()
        sum += random()
    return sum/n
print(twice())

>  1.00003

As expected, it's 1.0.

Okay, now let's turn it on its head: draw random numbers between 0 and 1, and stop when the sum exceeds 1. What is the expected number of draws?

def stop_at(z=1.0, n=1000*1000):
    total_draws = 0.0
    for _ in range(n):
        trial_sum = 0.0
        num_draws = 0
        while True:
            trial_sum += random()
            num_draws += 1
            if trial_sum >= z: break
        total_draws += num_draws
    return total_draws/n
print(stop_at(1))

> 2.71758

This returns $ e $, the base of the natural logarithm! Why does it show up here?

Practicing college math

As a reminder, the definition of $ e $:

Why is this the expected value of the draws?

Let $ N $ denote the random variable which denotes the number of draws required to cross 1.0. The expected value:

The sum starts at $ k = 2 $ because we need at least 2 draws, $ P(N=k) = 0 $ for $ k = 1 $.

The first step is to realize that $ P(N=k) $, the probability that we stop at $k$, is the probability that the sum is less than $1$ at $k-1$ draws, and exceeds $1$ after the $k$-th draw. Let $U_i$ denote the $i$-th draw, and let $S_k$ denote the sum up to $k$, $ S_k = \sum\limits_{i=1}^{k}{ U_i } $.

Then:

Now some elementary probability theory:

With $ A = S_{k-1} < 1 $ and $ B = S_{k} \geq 1 $:

Obviously, $ P( S_{k-1} < 1 \land S_k < 1 ) = P( S_k < 1 ) $, so:

Moving terms:

So:

Now we just need to figure out the formula for $ P( S_k < 1 ) $.

This is easiest solved geometrically. For $k=2$, $ P( S_k < 1 ) $ is the triangle area inside the x-y unit square where $x+y < 1$, which is clearly $1/2$. For $k=3$, $ P( S_k < 1 ) $ is the simplex volume inside the x-y-z unit square where $ x+y+z < 1 $. The simplex has as its base the previous triangle defined by $x+y < 1$, and has unit height.

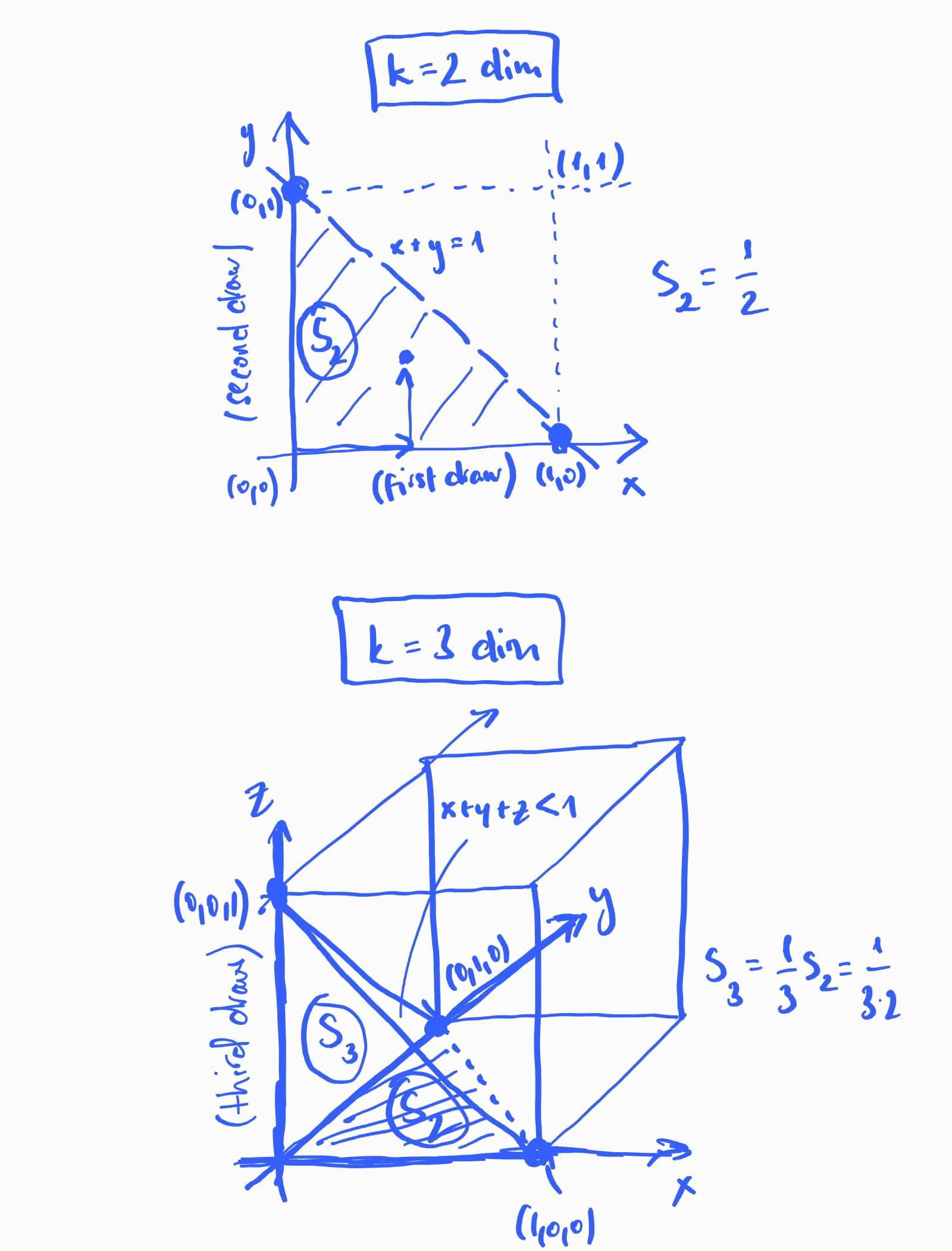
The general formula for the area of triangles (volumes of simplexes) with unit height in $k$ dimensions is $ V = A \times k $, where A is the area (volume) of the base, which is the same formula for $k-1$. Inductively, this means that:

We have the factorial from the definition of $e$! Now we apply a simple identity of the factorial, $ k! = k \times (k-1)! $ to our formula:

We're almost done:

Let $j = k-1$:

Let $n = j-1$:

Varying the stopping threshold

We saw above that if we stop at $z=1$, we need an average of $e$ draws. What if we want to stop at $z=2$ or $z=3.14$? What is the $E(N_z)$, the average number of draws required if we want to stop at $z$?

import matplotlib.pyplot as plt

x = [x/10 for x in list(range(10, 50, 1))]
y = [stop_at(i, n=100*1000) for i in x]
fig, ax = plt.subplots()
ax.plot(x, y, marker='o')
ax.set(xlabel='z', ylabel='average draws',
       title='E(N_z)')
ax.grid()
plt.show()

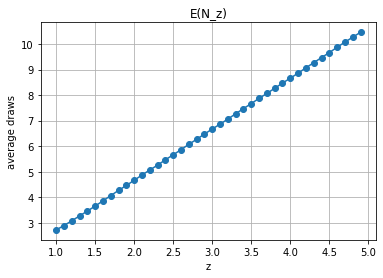
This is intuitive: if we need $e$ draws to reach $z$, and each additional draws averages $0.5$, so $E(N_z) = f(z) = e + 2(z-1)$.

Sometimes it's good to exercise our brain (and $\LaTeX$ skills) to stay sharp!

The ipython notebook is here.