Investigating information storage in quantized Autoencoders with Pytorch and MNIST

Introduction

In this experiment I wanted to understand the compression ratio of Autoencoders: how much information (how many bits) does an Autoencoder encode in the encoding dimensions? Let's say an autoencoder is able to encode a 28x28 grayscale MNIST image (28x28x8 bits = 6272 bits) in a 32 dimensional encoding space with acceptable reconstruction loss. What is the compression ratio? With a CUDA/GPU, those 32 dimensions are actually 32 float32's, so it's 32x32 = 1024 bits, which corresponds to 6.1x (lossy) compression. But are all those 1024 bits really needed? Intuitively the entire float32 space is probably not used. A related question is, what is the "right" number of encoding dimensions to pick for Autoencoders?

The notebook is up on Github.

Experiment setup

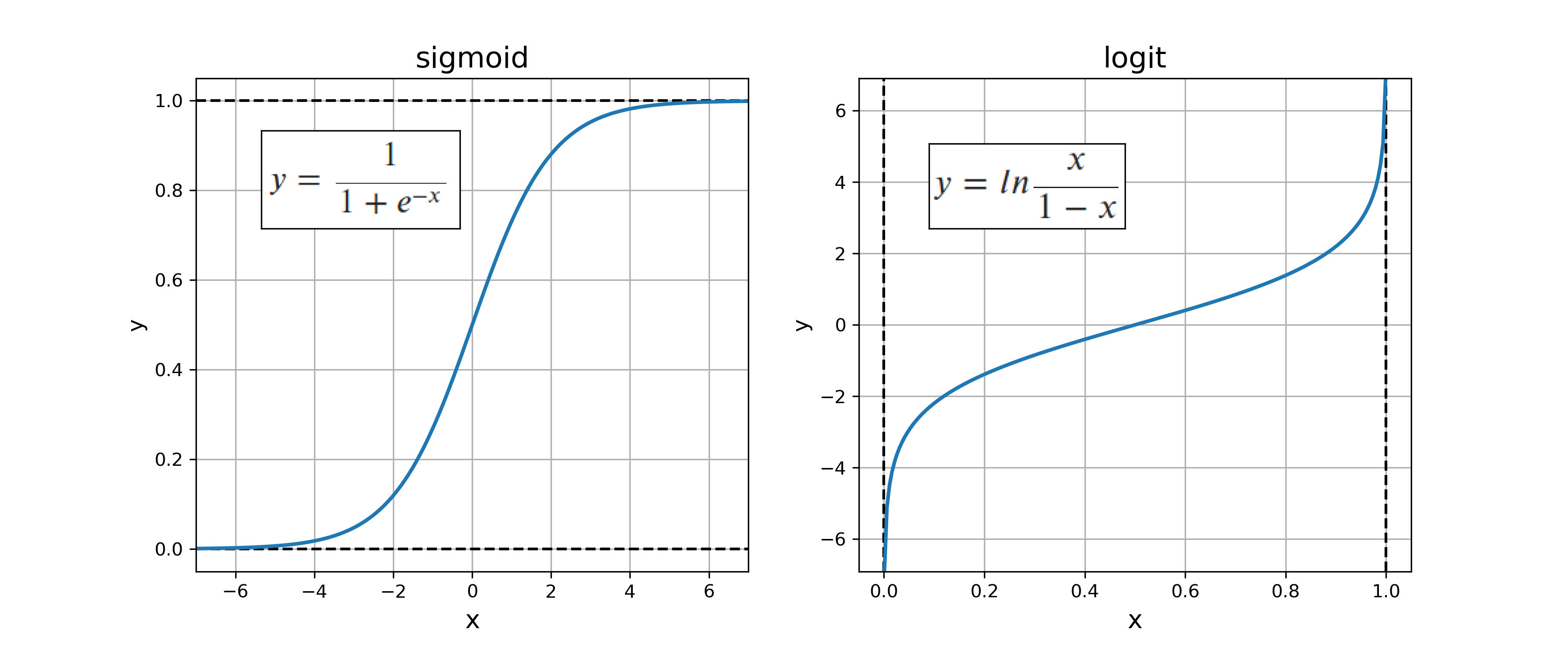
To answer these questions, I took a simple Autoencoder neural network with a Linear+ReLu encoder and a Linear+Sigmoid decoder layer. Since I will want to quantize the bits between the encoder and a decoder, I use the sigmoid() function to get the encoder's output to be between 0 and 1, and then the inverse, the logit() function before feeding back to the decoder.

Code

The code is a straightforward Autoencoder neural network implemented in Pytorch, with some additional transformations in the forward() function to implement quantization. The arrows mark the departure from a vanilla Autoencoder:

class Autoencoder(nn.Module):
    def __init__(self, encoding_dims):
        super(Autoencoder,self).__init__()
        self.encoder = nn.Sequential(
            nn.Flatten(),
            nn.Linear(img_dims*img_dims, encoding_dims),
            nn.ReLU(),
            )
        self.decoder = nn.Sequential(
            nn.Linear(encoding_dims, img_dims*img_dims),
            nn.Unflatten(1, (1, img_dims, img_dims)),
            nn.Sigmoid(),
            )
    def forward(self, x, quantize_bits=None):
        x = self.encoder(x)
        x = torch.sigmoid(x)                   <--- sigmoid
        if quantize_bits is not None:          <--- if not training
            x = round_bits(x, quantize_bits)   <--- .. then quantize the encoding
        x = torch.logit(x, eps=0.001)          <--- logit = inverse sigmoid
        x = self.decoder(x)
        return x

The function round_bits() quantizes the input number to 2**quantize_bits levels between 0 and 1:

def round_bits(x, quantize_bits):
    mul = 2**quantize_bits
    x = x * mul
    x = torch.floor(x)
    x = x / mul
    return x

The main training loop trains the Autoencoder for different encoding_dims, and then tests the reconstruction loss for various values of quantize_bits:

for encoding_dims in [4, 8, 16, 32, 64, 128, 256]:
    # train
    autoencoder = Autoencoder(encoding_dims=encoding_dims).to(device)
    distance = nn.BCELoss()
    optimizer = torch.optim.Adam(autoencoder.parameters(), lr=0.001)
    num_epochs = 50
    for epoch in range(num_epochs):
        for imgs, _ in autoencoder_train_dataloader:
            imgs = Variable(imgs).to(device)
            output = autoencoder(imgs)
            loss = distance(output, imgs)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
    # test
    distance = nn.MSELoss()
    for quantize_bits in [2, 4, 8, 16, 32]:
        loss = 0
        for imgs, _ in autoencoder_train_dataloader:
            imgs = Variable(imgs).to(device)
            with torch.no_grad():
                output = autoencoder(imgs, quantize_bits=quantize_bits)
            loss += distance(output, imgs)

Results

The results can be plotted to show the loss per encoding_dims, per quantize_bits:

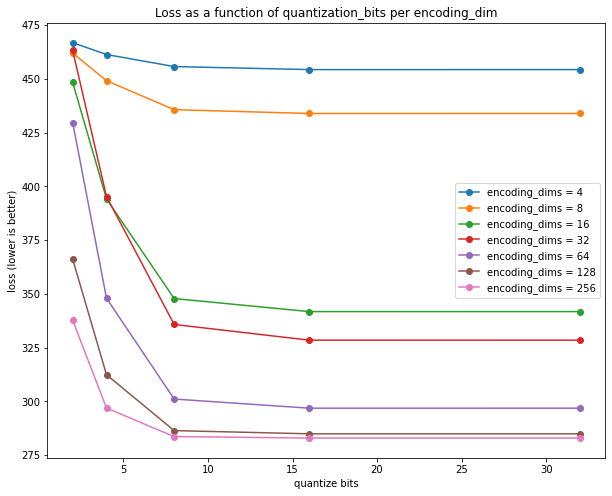
The plot shows that:

• each float32 in the encoding stores around 8 bits of useful information (out of 32), since all of the curves flatten out after 8 bits
• 128 dimensions is the maximum required, since the next jump to 256 yield no significant decrease in loss
• overall, based on these curves, encodim_dims = 64 and quantize_bits = 8 appears to be a good trade-off (total_bits = 64*8 = 512 bits)

Alternatively we can plot total_bits = encoding_dims * quantize_bits on the x-axis:

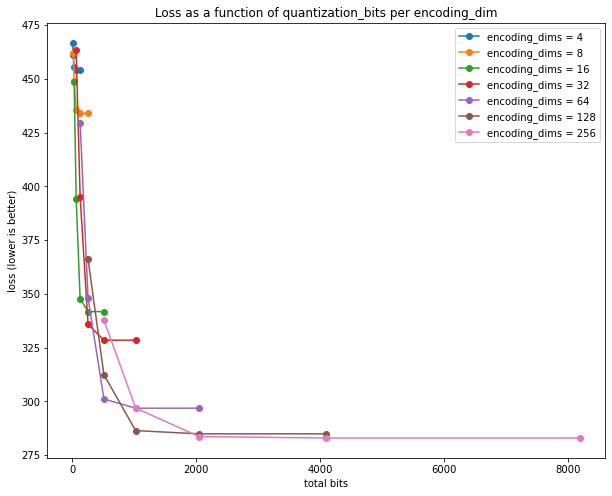
This re-affirms that 512 bits --- which corresponds to 12x (lossy) compression --- is a good trade-off, or 1024 bits for 10% less loss. Loss does not decrease significantly after 1024 bits, that appears to be best the Autoencoder can accomplish. For reference, the entire MNIST training dataset, uncompressed is 28*28*8 * 60*1000 / 8 = 47,040,000 bytes. After gzip compression, the file size is 9,912,422 bytes, for a lossless compression ratio of 4.7x.

In the next post, I will explore what we lose with the Autoencoder's lossy compression in terms of recognizability of the digits.