Introduction

After the 2020 US presidential election, the Trump campaign filed over 50 lawsuits and attacked the integrity of the elections by claiming there was voter fraud. One of the last lawsuits was filed in the Supreme Court of the United States (SCOTUS) by the state of Texas. Later more than a 100 Republican congressman joined the lawsuit in support. However, just a few days after filing, SCOTUS rejected the lawsuit because "Texas has not demonstrated a judicially cognizable interest in the manner in which another state conducts its elections." In other words, SCOTUS chose not to hear the lawsuit because the state of Texas has no business questioning how other states run their elections, but without opinionating on the merits of the lawsuit. So did the lawsuit have merit?

It was widely reported however that the lawsuit contained flawed statistical arguments. Having said that, note that the lawsuit contained lots of claims and arguments, this statistical one is just one of them.

The statistical claims can be summarized as:

1. Given the 2016 results of the Hillary Clinton - Donald Trump race in Georgia, the 2020 Joe Biden - Donald Trump results are very unlikely (and hence suspicious).
2. Given the early lead of Trump in Georgia in 2020, the final win of Biden is very unlikely (and hence suspicious).

The summary of this portion of the lawsuit is reproduced below (source, page 8):

The same less than one in a quadrillion statistical improbability of Mr. Biden winning the popular vote in the four Defendant States—Georgia, Michigan, Pennsylvania, and Wisconsin—independently exists when Mr. Biden’s performance in each of those Defendant States is compared to former Secretary of State Hilary Clinton’s performance in the 2016 general election and President Trump’s performance in the 2016 and 2020 general elections. Again, the statistical improbability of Mr. Biden winning the popular vote in these four States collectively is 1 in 1,000,000,000,000,0005.

And,

The probability of former Vice President Biden winning the popular vote in the four Defendant States—Georgia, Michigan, Pennsylvania, and Wisconsin — independently given President Trump’s early lead in those States as of 3 a.m. on November 4, 2020, is less than one in a quadrillion, or 1 in 1,000,000,000,000,000. For former Vice President Biden to win these four States collectively, the odds of that event happening decrease to less than one in a quadrillion to the fourth power (i.e., 1 in 1,000,000,000,000,0004).

2016 vs 2020

Let's look at the first one. The details start on page 20:

In plain english, it is:

• modeling Georgia voters across 2016 and 2020 with one random variable, with some probability p of voting Democratic (like a flip of a coin, except it's not an exactly fair coin)
• what is the probability that this one random variable (coin) produced the results of both 2016 and 2020?
• the probability (p-value) is very small, so it is very unlikely

Using the cited numbers we can compute the p-value directly with the Chi-squared test:

from scipy.stats import chi2_contingency
observations = [
    [1877963, 2474507],
    [2089104, 2461836],
]
# first column in 2016 results, second is 2020 results
p = chi2_contingency(observations)[1]
print('p = %.10f' % p)

Prints:

0.0000000000

There is zero probability that the null hypothesis is true, in other words, the voters in 2016 and 2020 cannot be modeled by the same random variable. So does this prove there was fraud?

No! Voters from 2016 to 2020 cannot be modeled as a random variable! Lots of things happened between 2016 and 2020 which affected Georgia voters. After all, they did not vote in 2020 for Biden based on what they thought of Hillary Clinton in 2016, and by 2020 they had a lot more information about Donald Trump.

The best way to prove this is to look at this historic Republican vs Democrat POTUS election chart for Georgia from the Wikipedia page United States presidential elections in Georgia:

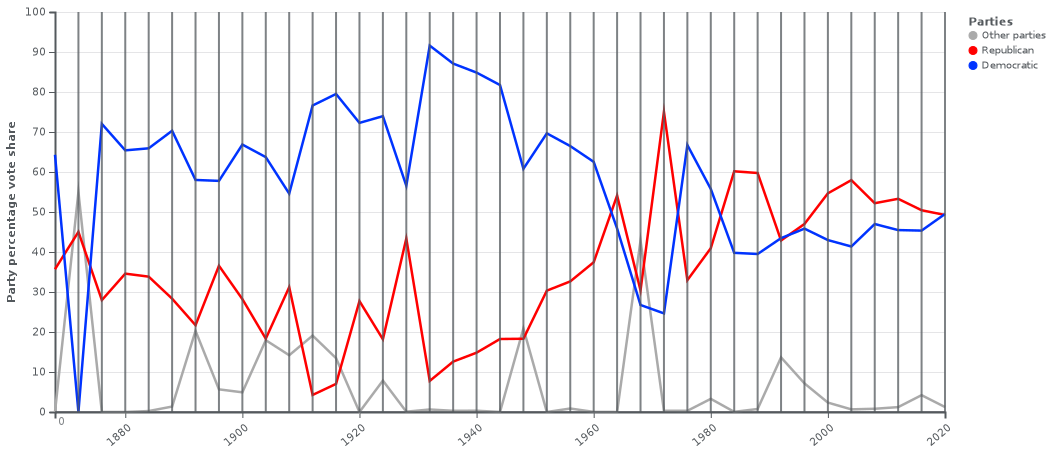
Does it look stable? No! Voters preferences change. Georgia used to be blue, then it was swingy, then it was mostly Republican, and now Biden by a thin margin. But this doesn't mean that there was constant voter fraud in the last 100 years as results changed.

Another quantitative way to show the absurdity of the argument is to compare the 2012 and the 2016 elections in Georgia. In both years, Georgia voted Republican, but:

from scipy.stats import chi2_contingency
observations = [
    [1773827, 1877963],
    [2078688, 2089104],
]
# first column in 2012, second is 2016
p = chi2_contingency(observations)[1]
print('p = %.10f' % p)

Again, prints:

0.0000000000

So again, there is zero probability that the null hypothesis is true, in other words, the voters in 2012 and 2016 cannot be modeled by the same random variable. So does this prove there was fraud in 2016 when Trump won? No. It just proves there are hundreds of thousands of Georgians who, from one election to the next:

• enter or exit the voting system (become eligible, move to Georgia, move away, die)
• change their vote
• do or do not vote

Early vs late counted votes

Here, the longer version of the argument with computational results, from the lawsuit:

Here the problem is the same as above. Votes from different counties and method of voting (in-person, mail-in) cannot be modeled by the same random variable. The fact that the results turned as votes were counted is simply a result of votes being counted faster or slower per county and per method of voting. In most counties, in-person votes were counted first, and mail-in votes were counted later, and different counties report their results at different speeds.

The statistical argument here would only hold if all the ballots in Georgia, from all the counties and all methods:

1. were first collected
2. put in a giant pile
3. the pile were thoroughly shuffled
4. votes randonly drawn from the pile one by one, and counted

Similar to how balls are mixed and drawn in a lottery drawing:

In this case, after randomization, it's correct to expect that whatever result we see after the first million votes are counted is representative of the final result, and the second million votes counted should yield very similar results as the first million --- assuming our random shuffle truly worked. But this is not how votes are counted in real life.

Conclusion

This is a beautiful example of making statistics lie. In the examples above, using scipy.stats illustrates this: statistics is like library function, we put in numbers, it returns back numbers, but it's up to us to interpret and explain them. We can make misleading and bogus assumptions and mischaracterize the results, or even put in bogus numbers. Statistics and library functions will never speak up.