Playing Go with supervised learning in Pytorch

Introduction

AlphaGo and AlphaGo Zero are tour-de-force demonstrations of the power of Deep Learning combined with Reinforcement Learning.

The new book Deep Learning and the Game of Go walks the reader through the steps of building an AlphaGo-like Go playing agent, starting from a completely randomized bot (but one which knows the rules of the game), to eventually a full-blown agent that learns with Reinforcement Learning. I’ve been reading it, it’s great, highly recommended.

One of the intermediate chapters in the book (Chapter 7) shows how to build a Deep Learning agent using supervised learning. In other words, given historic games between strong players (humans or bots) let a deep neural network learn to play good moves. In the context of building Go bots, the idea is not to use the output of the neural network directly. Instead, this output of the neural network can be used to build a bot that uses Monte Carlo Tree Search, as does AlphaGo.

The idea behind Monte Carlo tree search in games like Go is simple. When the bot has to make a move, there are a number of possibilites to place the next stone on the board. In MCTS, before making the actual move, the bot tries a number of moves in simulation, then switches sides, makes the next move, and so on; based on the outcome of these simulations (or, a score assignment is the game is not over), it weighs its options, and selects the next move accordingly. What makes Go hard, even harder than Chess, is that there are a lot of moves to try! Trying all valid moves is computationally infeasible, so the bot needs some help to select and prune interesting parts of the tree.

This is where a neural network using supervised learning is useful. If we train it on historic games, we get an agent which can return the top-N moves, which we can use in a MCTS setting. In order to not limit the bot too much by historics, it can optimistically also use an epsilon-greedy explore/exploit mechanism to find other interesting moves.

The book uses Keras in its examples. Inspired by the book, I wanted to see what it’s like to do this with Pytorch. The notebooks are up on Github.

Getting historic gameplay data

The site u-go.net lists many years worth of games between strong players (6d or better). The files are zipped, and inside we find a sgf file for each game. Fortunately, there is a Python library called sgfmill which makes opening and processing sgf game files simple.

import os

## download:
# curl https://u-go.net/gamerecords/ | grep 'https://dl.u-go.net/gamerecords/' | grep zip | cut -d'"' -f 2 | awk '{ print "wget " $1 }' | sh
## extract:
# ls -l | awk '{ print "unzip " $9 }' | sh

GAMEFILES_PATH = '<something>'

game_files = []
for r, d, f in os.walk(GAMEFILES_PATH):
    for file in f:
        if '.sgf' in file:
            game_files.append(os.path.join(r, file))

print('Total games: %s'  % len(game_files))

We use these games to create the training (and test) set. We loop though each move in each game, and create the map board -> next move. This is the mapping we want our neural network to learn.

from sgfmill import sgf, sgf_moves

def make_data_points(game_files):
    data_points = []
    for i, game_file in enumerate(game_files):
        print('Processing %s/%s: %s' % (i, len(game_files), game_file))
        with open(game_file) as f:
            contents = f.read().encode('ascii')
            game = sgf.Sgf_game.from_bytes(contents)
            board, plays = sgf_moves.get_setup_and_moves(game)
            for color, move in plays:
                if move is None: continue
                row, col = move
                tp = data_point(board, move, color)
                data_points.append(tp)
                board.play(row, col, color)
    return data_points

NUM_TRAINING_GAMES = 1000
NUM_TEST_GAMES = 100

training_game_files = game_files[:NUM_TRAINING_GAMES]
test_game_files = game_files[-NUM_TEST_GAMES:]
training_points = make_data_points(training_game_files)
test_points = make_data_points(test_game_files)

The code above calls data_point(), which actually constructs the desired representation, shown below.

Encoding data

Encoding the board positions is simple. Go is played 19x19 grid, and each grid point is either empty, occupied by white or occupied by black. We create 19x19 float arrays, where empty is 0.0, the player who goes next is encoded 1.0, the opponent is encoded -1.0. This way both white’s and black’s moves can be used for training. The move is the grid location of the next move, encoded in a one-hot vector of 19x19=361 length.

import torch

BOARD_SIZE = 19

def data_point(board, move, color):
    board_array = torch.zeros((1, BOARD_SIZE, BOARD_SIZE), dtype=torch.float32, device=device)
    for p in board.list_occupied_points():
        board_array[0, p[1][0], p[1][1]] = -1.0 + 2 * int(p[0] == color)
    return board_array, move[0]*BOARD_SIZE+move[1]

class GoDataset(data.Dataset):
    def __init__(self, data_points):
        self.data_points = data_points
    def __getitem__(self, index):
        return self.data_points[index][0], self.data_points[index][1]
    def __len__(self):
        return len(self.data_points)

training_dataset = GoDataset(training_points)
test_dataset = GoDataset(test_points)
train_loader = torch.utils.data.DataLoader(training_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1000, shuffle=True)

Neural network model

The neural network is a relatively simple Convolutional Neural Network, since we want it to learn 2D spatial patterns on the board. As usual, we use ReLu for nonlinearities. Interestingly, unlike with image recognition CNNs like the one I built for MNIST and CIFAR-10, on this one I had to use dropouts, ie. randomly turning off a fraction p of weights during each training run. Without dropouts, the model overfit the training data, but was performing barely beyond random guessing on test data.

The structure is:

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=9, stride=1, padding=4)
        self.conv2 = nn.Conv2d(in_channels=32, out_channels=32, kernel_size=7, stride=1, padding=3)
        self.conv3 = nn.Conv2d(in_channels=32, out_channels=32, kernel_size=5, stride=1, padding=2)
        self.fc1 = nn.Linear(in_features=32*BOARD_SIZE*BOARD_SIZE, out_features=BOARD_SIZE*BOARD_SIZE)
        self.fc2 = nn.Linear(in_features=BOARD_SIZE*BOARD_SIZE, out_features=BOARD_SIZE*BOARD_SIZE)
        self.dropout = nn.Dropout(0.5)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = x.view(-1, 32*BOARD_SIZE*BOARD_SIZE)
        x = self.dropout(F.relu(self.fc1(x)))      # notice the dropout
        x = self.dropout(self.fc2(x))              # notice the dropout
        x = F.log_softmax(x, dim=1)
        return x

Note that this is a pretty big model. It has 1M+ parameters, almost all of them in the final two fully connected (FC) layers; this is why it is able to overfit low cardinality training data.

Training and test accuracy

This is a relatively big model, so it needs to be trained on a GPU. On my GTX 970, training on 3000 games (500,000 moves) takes about 6 hours. The model converges to about 75% accuracy on train data and 25% accuracy on test data. Note that random guessing would have 1/19^2 = 0.27% accuracy, so this is 100x better. Also, there is not neccesary one right play, so being different than the test data is okay.

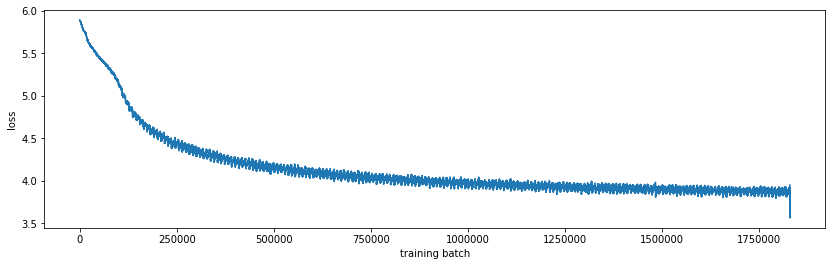
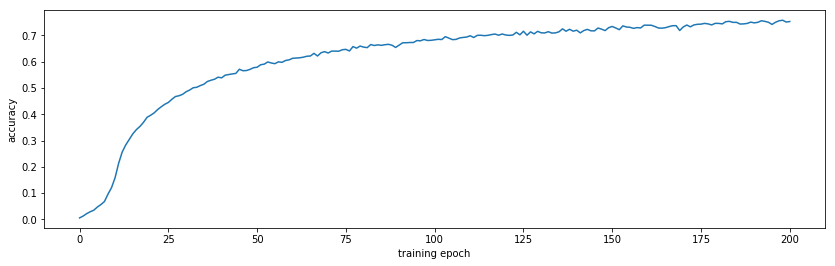
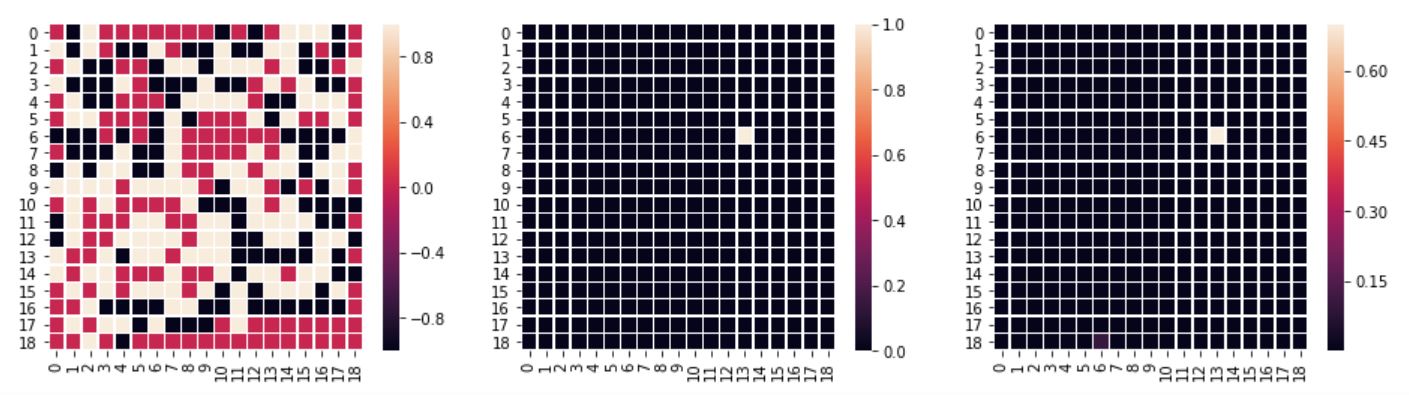
Examining the predictions was a bit surprising. The model has a softmax at the end, it’s predicting probabilities for each “class” (each of the possible moves). I thought that multiple good moves are identified by the model, which would make it useful in a MCTS algorithm. But that’s not what happens most of the time: the probabilities are usually “focused” on one move. Below are samples from the test data (left: board setup, center: actual move per test data, right: predicted move probabilities by model):

The test dataset's move is predicted:

Another move has a higher probability, but the test dataset's move also has a high probability (two maximums):

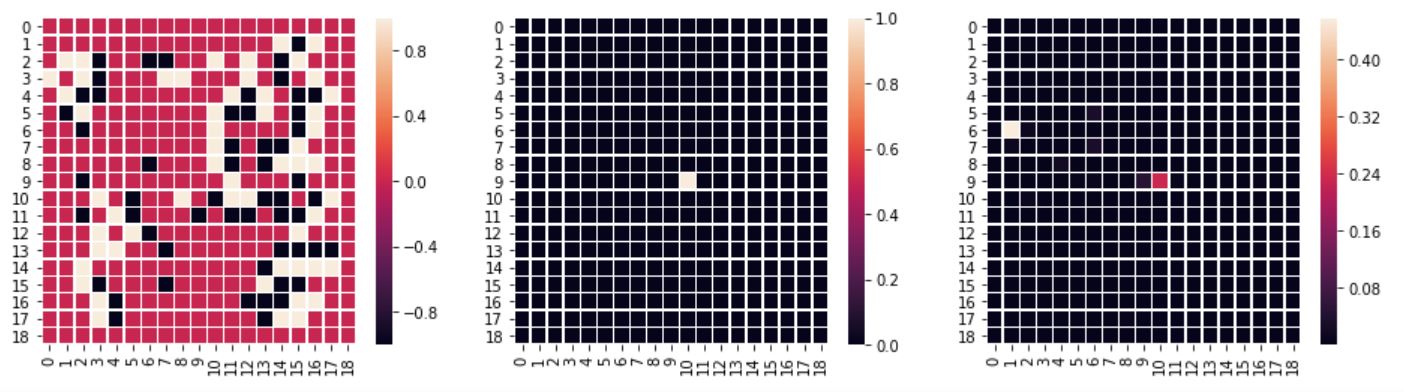
The test dataset's move is missed completely:

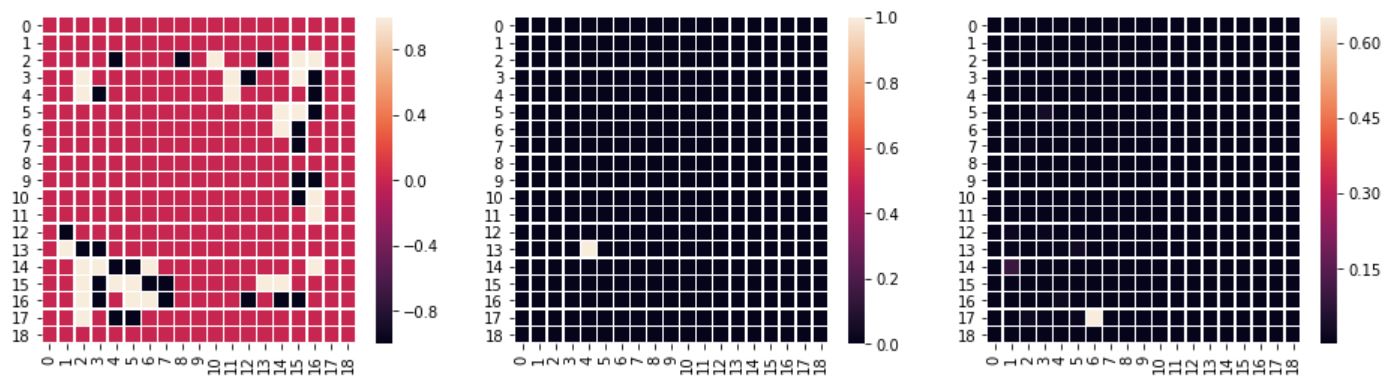
See the output here for more examples.

I didn’t try this, but this is probably not a problem: we can train multiple models on different training sets, and use the outputs of several models to guide the MCTS walk during simulation.

Conclusion

Neural networks are a great tool for well-defined problems with rich training data, and Go is like this. I didn’t pursue this specific supervised learning approach further, because this is not the most interesting way to build a Go bot. Here we are using other player’s moves to teach the network, which would potentially limit the agent’s strength and creativity. With Reinforcement Learning and self-play, as demonstrated by AlphaGo, it’s possible to build an agent that doesn’t use past gameplay data at all.

I don't actually play Go, so I plan to switch to Chess for further toy model building. Stay tuned!