Training a Pytorch Wasserstein MNIST GAN on Google Colab

Marton Trencseni - Wed 03 March 2021 - Data

Introduction

In the previous post, I trained a Classic GAN to produce MNIST digits using Pytorch. The results were okay, but a human discriminator can still tell these generated images apart from hand-written digits. In this post, I'll train a modification of the classic GAN called Wasserstein GAN. The Google Colab notebook is here.

Architecture

The Wasserstein GAN (WGAN) was introduced in a 2017 paper. This Google Machine Learning page explains WGANs and their relationship to classic GANs beautifully:

This loss function depends on a modification of the GAN scheme called "Wasserstein GAN" or "WGAN" in which the discriminator does not actually classify instances. For each instance it outputs a number. This number does not have to be less than one or greater than 0, so we can't use 0.5 as a threshold to decide whether an instance is real or fake. Discriminator training just tries to make the output bigger for real instances than for fake instances.

Because it can't really discriminate between real and fake, the WGAN discriminator is actually called a "critic" instead of a "discriminator". This distinction has theoretical importance, but for practical purposes we can treat it as an acknowledgement that the inputs to the loss functions don't have to be probabilities.

The loss functions themselves are deceptively simple:

Critic Loss: D(x) - D(G(z))

The discriminator tries to maximize this function. In other words, it tries to maximize the difference between its output on real instances and its output on fake instances.

Generator Loss: D(G(z))

The generator tries to maximize this function. In other words, It tries to maximize the discriminator's output for its fake instances. In these functions:

D(x) is the critic's output for a real instance.

G(z) is the generator's output when given noise z.

D(G(z)) is the critic's output for a fake instance.

The output of critic D does not have to be between 1 and 0.

Code

The Generator and Discriminator neural networks are exactly the same as in the classic GAN case!

class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()
        def block(in_feat, out_feat, normalize=True):
            layers = [nn.Linear(in_feat, out_feat)]
            if normalize:
                layers.append(nn.BatchNorm1d(out_feat, 0.8))
            layers.append(nn.LeakyReLU(0.2, inplace=True))
            return layers
        self.model = nn.Sequential(
            *block(opt.latent_dim, 128, normalize=False),
            *block(128, 256),
            *block(256, 512),
            *block(512, 1024),
            nn.Linear(1024, int(np.prod(img_shape))),
            nn.Tanh()
        )
    def forward(self, z):
        img = self.model(z)
        img = img.view(img.shape[0], *img_shape)
        return img

class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(opt.img_size ** 2, 512),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Linear(512, 256),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Linear(256, 1),
        )
    def forward(self, img):
        img_flat = img.view(img.shape[0], -1)
        validity = self.model(img_flat)
        return validity

The training code:

real_imgs = Variable(imgs.type(Tensor))
# train Discriminator
discriminator_optimizer.zero_grad()
# sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# generate a batch of images
fake_imgs = generator(z).detach()
# Adversarial loss
discriminator_loss = torch.mean(discriminator(fake_imgs)) - torch.mean(discriminator(real_imgs)) + 
discriminator_loss.backward()
discriminator_optimizer.step()
# clip weights of discriminator
for p in discriminator.parameters():
    p.data.clamp_(-opt.clip_value, opt.clip_value)
# train the generator every n_critic iterations
if i % opt.n_critic == 0:
    # train Generator
    generator_optimizer.zero_grad()
    # generate a batch of fake images
    critics_fake_imgs = generator(z)
    # Adversarial loss
    generator_loss = -torch.mean(discriminator(critics_fake_imgs))
    generator_loss.backward()
    generator_optimizer.step()

Results

Below are samples of MNIST digits produced by the GAN after 1, 5, 10, 50, 100, 150 and 200 epochs of training (an epoch is a full go through the MNIST dataset, consisting of 60K digits):

Epoch 1:

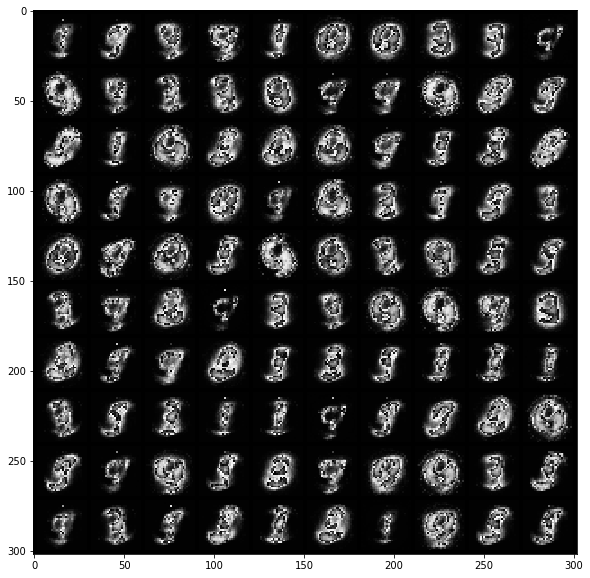
Wasserstein GAN Generated MNIST digits