Building a Pytorch Autoencoder for MNIST digits

Marton Trencseni - Thu 18 March 2021 - Data

Introduction

In the previous posts I was training GANs to auto-generate synthetic MNIST digits:

Here I take a step back to a simpler idea from unsupervised learning, Autoencoders. The idea is simple: take the input, reduce the dimensionality toward the middle of the deep neural network in the encoder part, and then restore the original dimensionality in the second, decoder part. The network is then trained to attempt to restore the original input, which in this case is MNIST digits, with minimal loss.

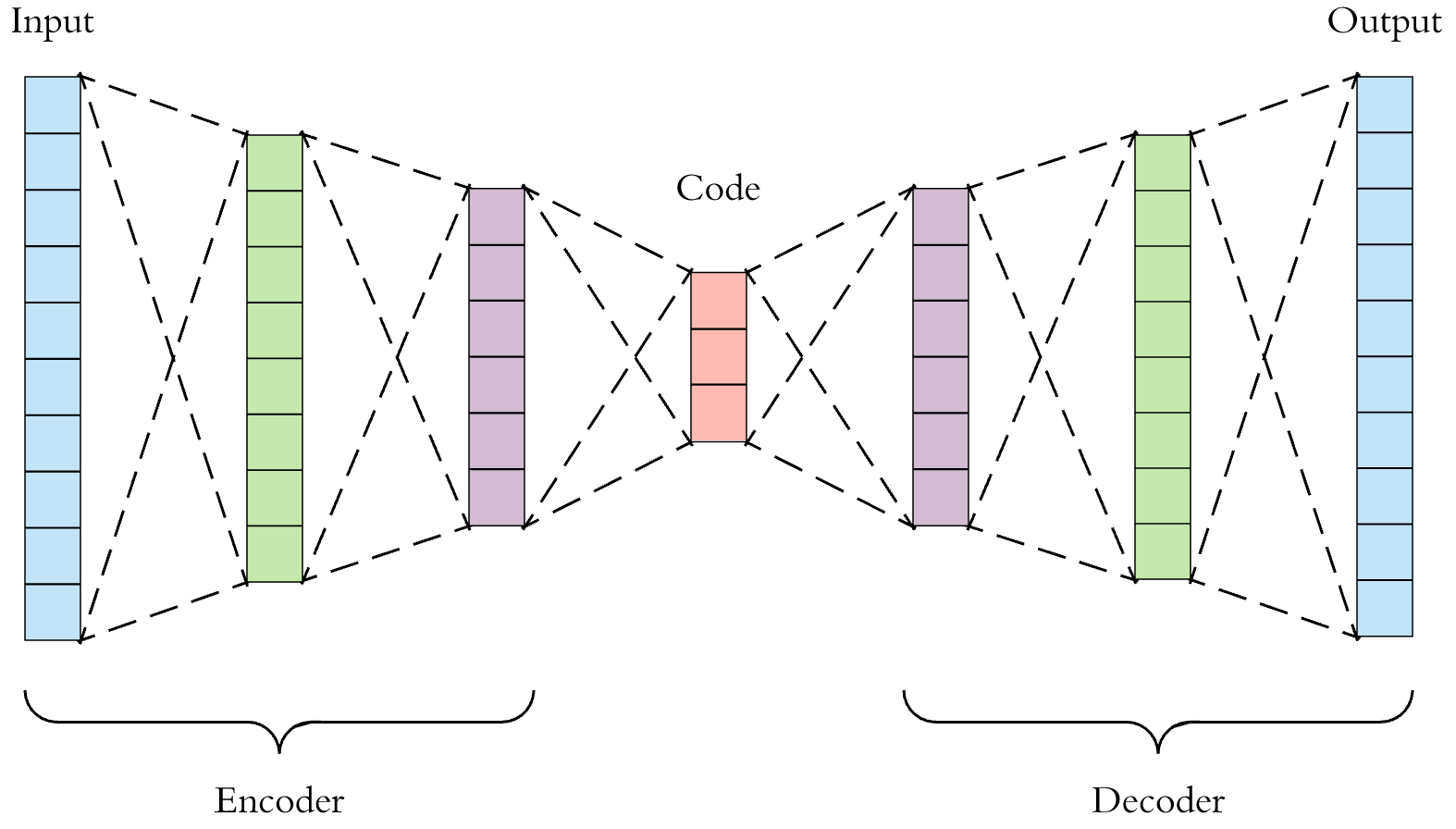
Autoencoder.

The Wikipedia explanation:

An autoencoder is a type of artificial neural network used to learn efficient data codings in an unsupervised manner. The aim of an autoencoder is to learn a representation (encoding) for a set of data, typically for dimensionality reduction, by training the network to ignore signal “noise”. Along with the reduction side, a reconstructing side is learned, where the autoencoder tries to generate from the reduced encoding a representation as close as possible to its original input, hence its name.

In this post, I will try to build an Autoencoder in Pytorch, where the middle "encoded" layer is exactly 10 neurons wide. My assumption is that the best way to encode an MNIST digit is for the encoder to learn to classify digits, and then for the decoder to generate an average image of a digit for each. The ipython notebook is here.

MNIST autoencoder.

Code

I will only show the relevant parts of the code. First, the Autoencoder model, split into an encoder and a decoder:

class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder,self).__init__()
        self.encoder = nn.Sequential(
            # 28 x 28
            nn.Conv2d(1, 4, kernel_size=5),
            # 4 x 24 x 24
            nn.ReLU(True),
            nn.Conv2d(4, 8, kernel_size=5),
            nn.ReLU(True),
            # 8 x 20 x 20 = 3200
            nn.Flatten(),
            nn.Linear(3200, 10),
            # 10
            nn.Softmax(),
            )
        self.decoder = nn.Sequential(
            # 10
            nn.Linear(10, 400),
            # 400
            nn.ReLU(True),
            nn.Linear(400, 4000),
            # 4000
            nn.ReLU(True),
            nn.Unflatten(1, (10, 20, 20)),
            # 10 x 20 x 20
            nn.ConvTranspose2d(10, 10, kernel_size=5),
            # 24 x 24
            nn.ConvTranspose2d(10, 1, kernel_size=5),
            # 28 x 28
            nn.Sigmoid(),
            )
    def forward(self, x):
        enc = self.encoder(x)
        dec = self.decoder(enc)
        return dec

Note that the forward() pass is decoder(encoder(x)), the only reason I separated the 2 parts of the network is that so I can peek at the the middle, encoded part, to see how it's encoding the digits.

The training loop:

distance = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

for epoch in range(num_epochs):
    for data in dataloader:
        img, _ = data
        img = Variable(img).cpu()
        output = model(img)
        loss = distance(output, img)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    print('epoch [{}/{}], loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))

Evaluation

Let's compare the activation of the 10 encoded neurons to the true labels of unseen MNIST test data:

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Autoencoder().to(device)
testset = tv.datasets.MNIST(root='./data',  train=False, download=True, transform=transform)
dataloader = torch.utils.data.DataLoader(testset, batch_size=10*1000, shuffle=True, num_workers=4)

confusion_matrix = np.zeros((10, 10))
for data in dataloader:
    img, labels = data[0].to(device), data[1].to(device) 
    imgs = Variable(imgs).cpu()
    encs = model.encoder(imgs).detach().numpy()
    for i in range(len(encs)):
        predicted = np.argmax(encs[i])
        actual = labels[i]
        confusion_matrix[actual][predicted] += 1

Note that the confusion matrix here is not a classical confusion matrix in the sense that it doesn't necessarily have to be an identity matrix, since the encoded neurons ordering is arbitrary. In the best case, the resulting matrix can be row-column-reordered and normalized to be an identity matrix (assuming balanced data).

Plotting the confusion matrix, where rows are the actual digits (0-9) and columns are the indices of the most active neuron (0-9):

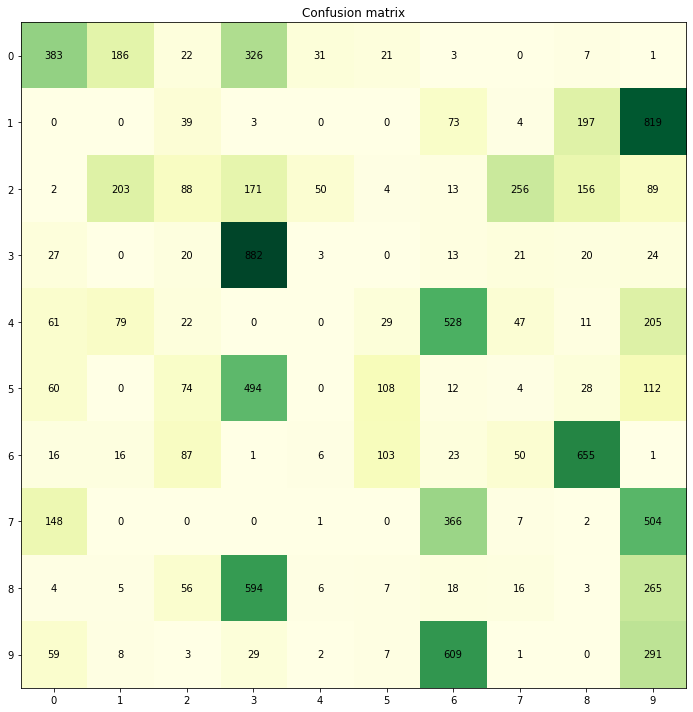
MNIST autoencoder.

For example, for row 6 (actuall the seventh, since numbering starts at 0), we can see that column 8 is the most active. And conversely, most of the time column 8 is active is for row 6. So the model learned to tell 6s apart from the rest, with some accuracy.

However, this unsupervised classifier is very far from perfect. For example, column 3 activates for actuals 3, 5, and 8. That's no surprise, since these digits actually look alike. To gauge how successful the encoding is, we can pick, for each endoding, the most likely actual value:

classifier = {
    # enc -> predict
    0: 0,
    1: 2,
    2: 2,
    3: 3,
    4: 2,
    5: 5,
    6: 9,
    7: 2,
    8: 6,
    9: 1,
}

If we run a prediction model on the encoder with this mapping, we get an accuracy of 40%. It's much worse than the 99% than is achievable with supervised learning, but it's much better than the 10% we'd expect from random chance.

Conclusion

This was an experiment in seeing whether an autoencoder can learn, without supervision, to recognize the 10 digits in MNIST, since that would probably be an optimal encoding --- assuming the images for each digit class are not too different in the MNIST data, so that encoding in that way is optimal. The result is worse than I expected, even after I asked for help on Stackoverflow and I merged those solutions with my own. I suspect with more tweaking of the network and the training loop, at least 2/3 accuracy could be achieved. If I can improve this model significantly, I will re-visit this topic in a future post.

pytorch autoencoder mnist