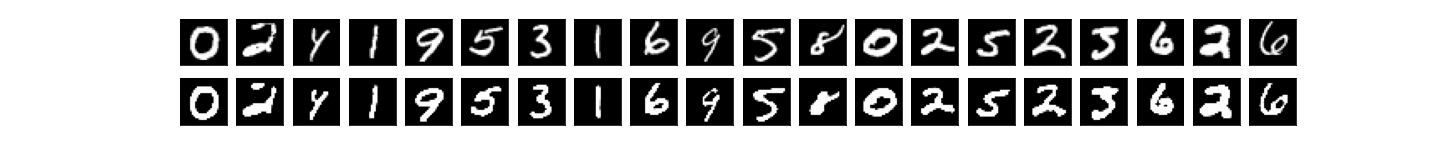Classification accuracy of quantized Autoencoders with Pytorch and MNIST
Marton Trencseni - Fri 09 April 2021 - Machine Learning
Introduction
In the previous post I investigated the information contents, in bits, that Autoencoders store. I took MNIST digits, trained a simple Autoencoder neural network to first encode the pictures in 4..256 dimensions, where each vector element is a float32. Then I took the elements, and quantized them to 2..32 bits accuracy, and measured the reconstruction loss as a function of encoding dimension and quantization:
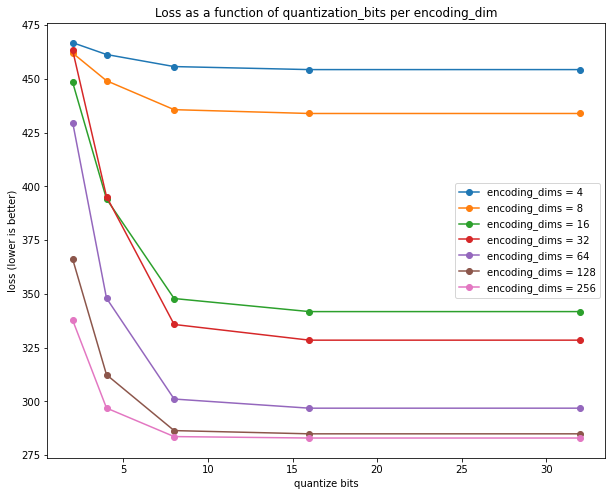
Based on the plot, my conclusion was:
... 512 bits --- which corresponds to 12x (lossy) compression --- is a good trade-off, or 1024 bits for 10% less loss. Loss does not decrease significantly after 1024 bits, that appears to be best the Autoencoder can accomplish.
However, this conclusion is just eye-balled based on the plots leveling off. The y-axis here is loss, which is related to pixel distance between original and reconstruction, but it's actually hard to know what a loss of ~300 really means. Also, this loss is not straightforward pixel distance, since it's standard practice to re-scale and normalize MNIST images to help the neural networks:
tv.datasets.MNIST(..., transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)), <--- image pixels are re-scaled
]))
A better approach to quantify the "loss" is to run a classifier on the output and see how recognizable the digits are in terms of Accuracy %.
Experiment setup
The MNIST dataset contains a total of 70,000 digits. Usually the first 60,000 are used for training, the remaining 10,000 for testing. Here, I will use:
- 30,000 for training a CNN classifier, as in this earlier post
- 30,000 for training a Autoencoder, like in the previous post
- 10,000 for testing, how the classifier performs on quantized digits coming from the Autoencoder
Then, I follow the same strategy as previously, but instead of using loss as a metric, I run the quantized Autoencoder's output through the classifier, and plot the accuracy as a as a function of encoding dimension and quantization.
Code
First, some helpers to split the dataset into 3 parts:
class MNISTPartialTrainDataset(Dataset):
def __init__(self, root, num_samples=None, offset=0):
self.base_dataset = tv.datasets.MNIST(root=root, train=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
]))
if num_samples is None:
self.num_samples = len(self.base_dataset)
else:
self.num_samples = min(num_samples, len(self.base_dataset)-offset)
self.offset = offset
def __len__(self):
return self.num_samples
def __getitem__(self, idx):
return self.base_dataset[self.offset+idx]
class MNISTPartialTestDataset(Dataset):
def __init__(self, root, num_samples=None, offset=0):
self.base_dataset = tv.datasets.MNIST(root=root, train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
]))
if num_samples is None:
self.num_samples = len(self.base_dataset)
else:
self.num_samples = min(num_samples, len(self.base_dataset)-offset)
self.offset = offset
def __len__(self):
return self.num_samples
def __getitem__(self, idx):
return self.base_dataset[self.offset+idx]
The classifier is a vanilla CNN:
class Classifier(nn.Module):
def __init__(self):
super(Classifier, self).__init__()
self.model = nn.Sequential(
nn.Conv2d(1, 20, 5, 1),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(20, 50, 5, 1),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Flatten(),
nn.Linear(4*4*50, 500),
nn.ReLU(),
nn.Linear(500, 10),
nn.LogSoftmax(),
)
def forward(self, x):
return self.model(x)
We train the classifier on the first 30,000 MNIST digits:
classifier = Classifier().to(device)
distance = nn.NLLLoss()
optimizer = torch.optim.SGD(classifier.parameters(), lr=0.01, momentum=0.5)
num_epochs = 20
for epoch in range(num_epochs):
for data, target in classifier_dataloader:
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = classifier(data)
loss = distance(output, target)
loss.backward()
optimizer.step()
print('epoch {:d}/{:d}, loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()), end='\r')
correct = 0
classifier = classifier.to('cpu')
for data, target in classifier_dataloader:
output = classifier(data)
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
print('Classifier train accuracy: {:.1f}%'.format(100*correct/len(classifier_dataloader.dataset)))
The classifier achieves 99.8% train accuracy, as expected:
Classifier train accuracy: 99.8%
Now the Autoencoder, exactly the same as before:
class Autoencoder(nn.Module):
def __init__(self, encoding_dims):
super(Autoencoder,self).__init__()
self.encoder = nn.Sequential(
nn.Flatten(),
nn.Linear(img_dims*img_dims, encoding_dims),
nn.ReLU(),
)
self.decoder = nn.Sequential(
nn.Linear(encoding_dims, img_dims*img_dims),
nn.Unflatten(1, (1, img_dims, img_dims)),
nn.Sigmoid(),
)
def forward(self, x, quantize_bits=None):
x = self.encoder(x)
x = torch.sigmoid(x)
if quantize_bits is not None:
x = round_bits(x, quantize_bits)
x = torch.logit(x, eps=0.001)
x = self.decoder(x)
return x
The main loop is very similar to before, except there is an additional step, where the trained classifier is run on the Autoencoder's output digits:
results = []
for encoding_dims in [4, 8, 16, 32, 64, 128, 256]:
# train autoencoder, code omitted
...
# test
for quantize_bits in [None, 2, 4, 8, 16, 32]:
correct = 0
autoencoder = autoencoder.to('cpu')
for imgs, labels in autoencoder_test_dataloader:
ae_imgs = autoencoder(imgs, quantize_bits=quantize_bits)
output = classifier(ae_imgs)
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(labels.view_as(pred)).sum().item()
accuracy = correct/len(autoencoder_test_dataloader.dataset)
results.append((encoding_dims, quantize_bits, accuracy))
Results
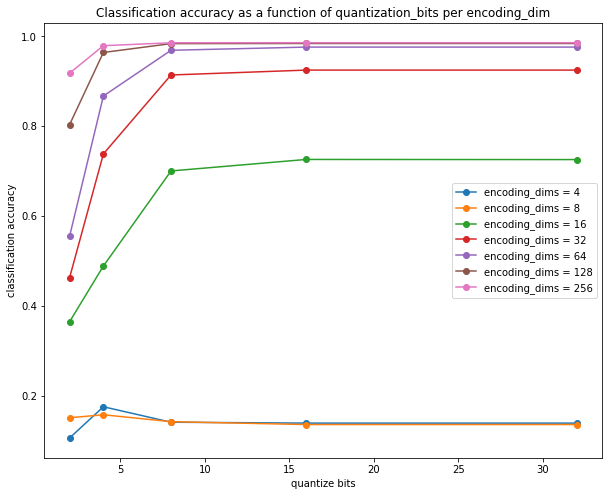
The results can be plotted to show the accuracy of the classifier per encoding_dims, per quantize_bits:
Alternatively we can plot total_bits = encoding_dims * quantize_bits on the x-axis:
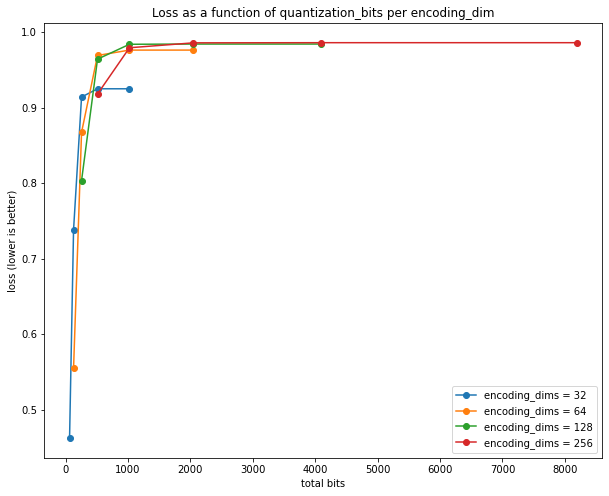
The plots re-affirm what I read off the previous plots, that
- each
float32in the encoding stores around 8 bits of useful information (out of 32), since all of the curves flatten out after 8 bits - 128 dimensions is the maximum required, since the next jump to 256 yield no significant increase in accuracy
- overall, based on these curves,
encodim_dims = 64andquantize_bits = 8appears to be a good trade-off (total_bits = 64*8 = 512 bits)
However, now it's easier to quantify:
- at
encodim_dims = 64andquantize_bits = 8(total_bits = 64*8 = 512 bits), the classifier achieves 97% accuracy, which is still great - at higher
total_bits, and with no quantization at all, the classifier achieves 98% on these unseen, encoded-than-decoded images, which is the same 98% we get without no quantization at all
Finally, to visually see what happens when we autoencode and quantize, a sample of the Autoencoder's output, for encoding_dims=64 and various quantization levels:
encodim_dims = 64, quantize_bits = 2 -> total_bits = 128, accuracy = 60%:
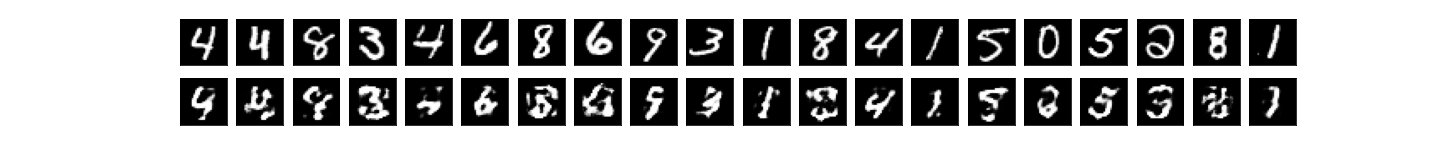
encodim_dims = 64, quantize_bits = 4, total_bits = 256, accuracy = 90%:
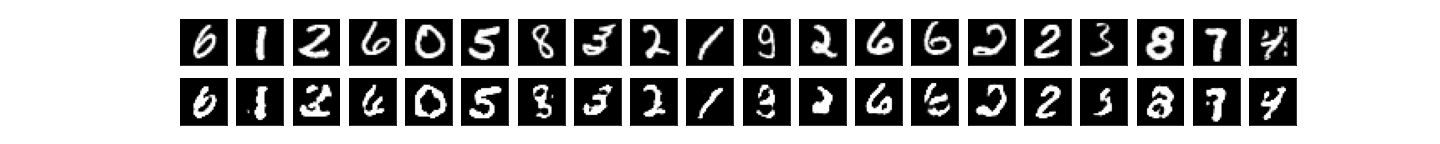
encodim_dims = 64, quantize_bits = 8, total_bits = 512, accuracy = 97%:
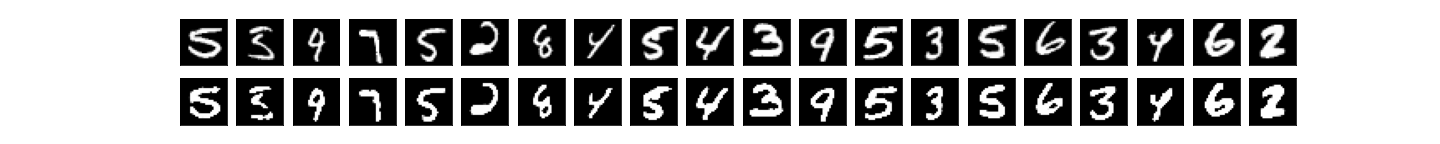
encodim_dims = 64, quantize_bits = 16, total_bits = 1024, accuracy = 98%:
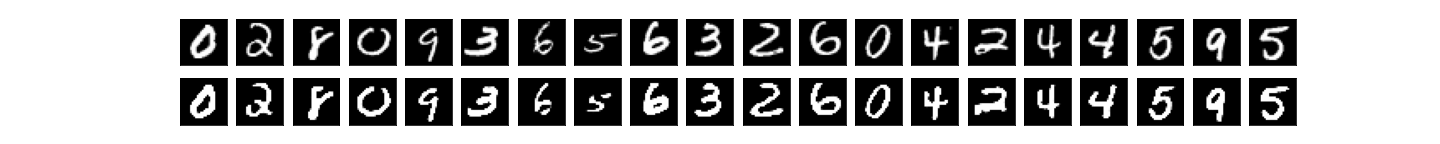
encodim_dims = 64, quantize_bits = 32, total_bits = 2048, accuracy = 98%:
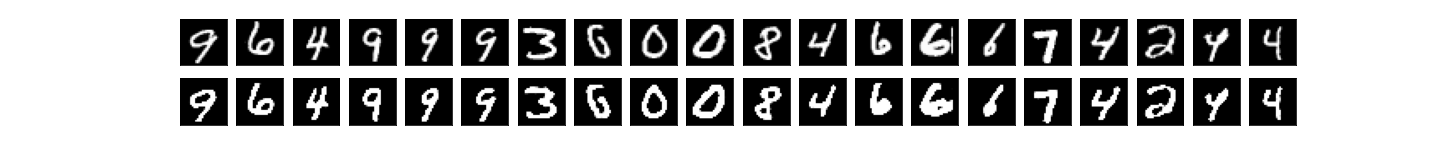
encodim_dims = 64, not quantized, accuracy = 98%: